Chapter 13: Navigation

Upon completion of this chapter you will be able to describe the basic constituents of spacecraft navigation including the role of the mission reference trajectory, the need for orbit determination, and flight path control via propulsive maneuvers. You will be able to recognize four distinct Deep Space Network (DSN) data types used in navigation, and be able to describe spacecraft trajectory correction maneuvers, orbit trim maneuvers, and deep-space maneuvers.

Spacecraft navigation comprises three main aspects:

A spacecraft is always orbiting something. On the launch pad, it is orbiting the Sun along with Earth. A spacecraft on its way to a distant planet is following its own orbit about the Sun. Spacecraft that have landed on a planet or other body are still orbiting the Sun. Some spacecraft are orbiting planets or other bodies, while those bodies themselves are orbiting the Sun. A few spacecraft have achieved enough velocity that they will never return to the Sun — their paths are hyperbolic with respect to the Sun — and so they are orbiting the center of our galaxy, just as the Sun itself is.

At the heart of JPL's navigation legacy is its navigation software suite, which is the embodiment of 50 years of know-how, developed for and tested by actual deep-space missions.

Those who take on the challenge of designing, coding, testing, and implementing JPL's remarkable navigation software routinely reach into the world of abstract mathematics.

With a firm grasp on formulations from the likes of Galileo, Newton, Kepler, Gauss, Tsiolkovsky, Hohmann, Oberth, Einstein, and so many others, they architect, build, and maintain applications programs that reliably deliver many a prized spacecraft along its reference trajectory in the solar system -- having generated the reference trajectory in the first place, of course.

There is an iterative relationship between the engineers who build the navigation software tools and those on the front lines actually flying missions.

Obviously, an operational navigator needs navigation software to fly a mission. Perhaps less apparent, the software engineers need navigators to take their software through the ropes of a real mission, so that they can ferret out the bugs, stretch the software to its limits, and request new features. The end result of this loop is a robust software suite that can withstand the rigors of real space missions.

The job of the orbit determination team is to keep track of where the spacecraft has been (orbit reconstruction), where it is currently (orbit determination), and where it will be in the future (orbit prediction). The spacecraft is always drifting away from its planned flight path because of disturbances it encounters in space. Even small disturbances, like the pressure of Sunlight on the spacecraft, can add up over time and push the spacecraft off course.

The mission designers do their best to account for these disturbances while creating the reference trajectory, but there is no accounting for randomness and unpredictability of the real world. To further complicate matters, once the spacecraft leaves the launch pad, it can no longer be directly observed. Orbit determination analysts must process various forms of tracking data that are tied mathematically to the evolution of the spacecraft orbit, to figure out its position at any given time.

Reconstructing the path flown is essential to making sense of scientific data returned, whether for interpreting the spacecraft's passage through planetary magnetospheres or rings, or for interpreting imaging results. One imaging technique in particular, that of synthetic aperture radar, SAR, requires ultra-precise trajectory reconstruction.

Another essential use is the creation of predicts, which are data sets delivered to the DSN that predict the location in the sky for the antennas to look, and the radio frequencies for DSN to use in acquiring and tracking the spacecraft. Reconstruction of the propulsive maneuvers themselves allows magnitude and pointing biases to be identified, quantified, and accommodated in future maneuver designs. The processes involved in navigation are indeed iterative in many ways.

An interplanetary spacecraft's course is mostly set once the launch vehicle has fallen away. From that point on, the spacecraft can make only very small corrections in its trajectory by firing small engines or thrusters. Often the largest complement of propellant that a spacecraft carries is reserved for orbit insertion at its destination.

Once the orbit determination team has a good estimate for the current location of the spacecraft, the flight path control team is responsible for evaluating how far the spacecraft has drifted from the reference trajectory, and for designing a maneuver to get the spacecraft back on course. The result of this maneuver design is a ΔV (delta-V) vector, which stands for change in velocity. This ΔV vector represents the direction and magnitude of the required change in the spacecraft velocity which must be accomplished to get the spacecraft back on course; a specific point in time is also indicated. Once in hand, this data is given over to the spacecraft engineering team, which includes attitude control engineers, propulsion system engineers, and others. They decompose the vector and the timing into the requirements for spacecraft pointing and rocket-engine or thruster firings.

In general, a smaller-magnitude change would be required immediately following an event like a planetary flyby, than would be required if the spacecraft were allowed to continue to drift off course. This must be balanced against the need to obtain perhaps a few days of DSN tracking, though, to ensure an accurate orbit determination.

The spacecraft team creates a set of commands to accomplish the correction, and carries out any needed testing. The commands are then uplinked to the spacecraft, which in turn performs the maneuver.

After a maneuver has been performed, the cycle repeats. Perhaps the thrusters were slightly misaligned, or the engine cutoff was a few milliseconds too late. The orbit determination team must take more tracking data to verify the maneuver performance. This iterative relationship between orbit determination and flight path control continues without pause through the lifetime of a flight mission. The spacecraft is constantly wandering off, and must be patiently nudged back on course.

During interplanetary cruise, a minor flight-path control maneuver is typically called a Trajectory Correction Maneuver, TCM. Generally, TCMs involve a ΔV magnitude on the order of meters per second, or sometimes tens of meters per second. For a spacecraft that is repeatedly orbiting a planet or other body, a ΔV maneuver is normally referred to as an Orbit Trim Maneuver, OTM. Typically, OTMs vary in magnitude from a few millimeters per second up to several meters per second.

Some ΔV maneuvers are "deterministic," which means that their execution, and at least a good estimate of their ΔV value, are known beforehand to be required for keeping to the reference trajectory. Other ΔV maneuvers are "stochastic," meaning that their execution, and their ΔV value, cannot be well predicted ahead, for example because of uncertainties inherent in a gravity-assist flyby. Sometimes a stochastic maneuver may be deemed unnecessary near real time, and can be cancelled.

A spacecraft's total ΔV capability is constrained due to the limited amount of propellant that a spacecraft can carry. If the mission plan for an interplanetary flight depends on a large-magnitude ΔV maneuver, for example if a gravity-assist flyby is not available at the desired point, that cardinal maneuver is typically called a Deep Space Maneuver, DSM. (A DSM is really just an especially large deterministic TCM.) The design of the spacecraft, as well as the selection of a launch vehicle, has to ensure that the spacecraft will carry sufficient propellant (ΔV capability) to cover any DSMs as well as routine TCMs and OTMs.

Cassini provides an example of the accuracy achieved in flight-path control maneuvers. The duration of Cassini's rocket or thruster firing for TCMs and OTMs has been executed within about 0.1% of the planned duration, and the pointing direction has been within about 7 milliradians (0.4 degrees) of the desired pointing. Over the course of seven years from launch to arrival at Saturn, Cassini executed seventeen TCMs. Once in orbit at Saturn, there have been three opportunities for OTMs during each orbit that includes an encounter with Titan or other body: one at apoapsis, and one each before and after a flyby. Each Titan flyby provides a gravity-assist to help shape Cassini's next orbit. There have been over four hundred OTM opportunities to date, and Cassini has needed to execute about three hundred of them. Many have been cancelled due to the accuracy of targeted flybys.

The ability to measure quantities that have a mathematical relationship to the motion of the spacecraft is a key component of navigation. The
meaningful measurements — the observables — we can make from earth of the spacecraft are:

Since these measurements are based on Earth, it is necessary that Earth's own orbital parameters and inherent motions be well known, so the measurements make sense in a Sun-centered (heliocentric) reference.

Some spacecraft can generate a fourth type of navigation data:

The everyday measurements of Doppler and range do not directly yield the lateral motion of a spacecraft deep in the solar system (if we define lateral motion as any component of motion except directly toward or away from earth.)

But we do have a very good understanding of how things move in space -- orbit models of spacecraft are built based on equations of motion from the likes of Kepler and Newton and Einstein. There aren't many ways of moving (in other words, trajectories) that can match up with a big batch of range and Doppler data acquired from various DSN station locations over a period or days, weeks or months.

The task is to apply measurements of Doppler and range to a model of a trajectory, and update that model to match all the measurements, to obtain a solution to the orbit determination problem. Gaining knowledge of lateral motion is then a process of iterating the model.

Measurements of the Doppler shift of a coherent downlink carrier provide the radial component of a spacecraft's earth-relative velocity. Doppler is a form of the tracking data type, TRK, provided by the DSN.

A uniquely coded ranging pulse can be added to the uplink to a spacecraft and its transmission time recorded. When the spacecraft receives the ranging pulse, it returns the pulse on its downlink. The time it takes the spacecraft to turn the pulse around within its electronics is known from pre-launch testing. For example, Cassini takes 420 nanoseconds, give or take 9 ns. There are many other calibrated delays in the system, including the several microseconds needed to go from the computers to the antenna within the DSN, which is calibrated prior to each use. When the pulse from the spacecraft is received at the DSN, its true elapsed time at light-speed is determined, corrections are applied for known and estimated effects of earth's ionosphere and atmosphere, and the spacecraft's distance is then computed. Ranging is also a type of TRK data provided by the DSN.

The spacecraft's position in the sky is expressed in the angular quantities Right Ascension and Declination. While the angles at which the DSN antennas point are monitored with an accuracy of thousandths of a degree, they are not precise enough to be used in determining a distant interplanetary spacecraft's position in the sky for navigation. DSN tracking antenna angles are useful only for pointing the antenna to the predicts given for acquiring the spacecraft's signal.

Fairly accurate determination of Right Ascension is a direct by-product of measuring Doppler shift during a DSN pass of several hours. Declination can also be measured by the set of Doppler-shift data during a DSN pass, but to a lesser accuracy, especially when the Declination value is near zero, i.e., near the celestial equator.

Better accuracy in measuring a distant spacecraft's angular position can be obtained by:

Very Long Baseline Interferometry (VLBI)

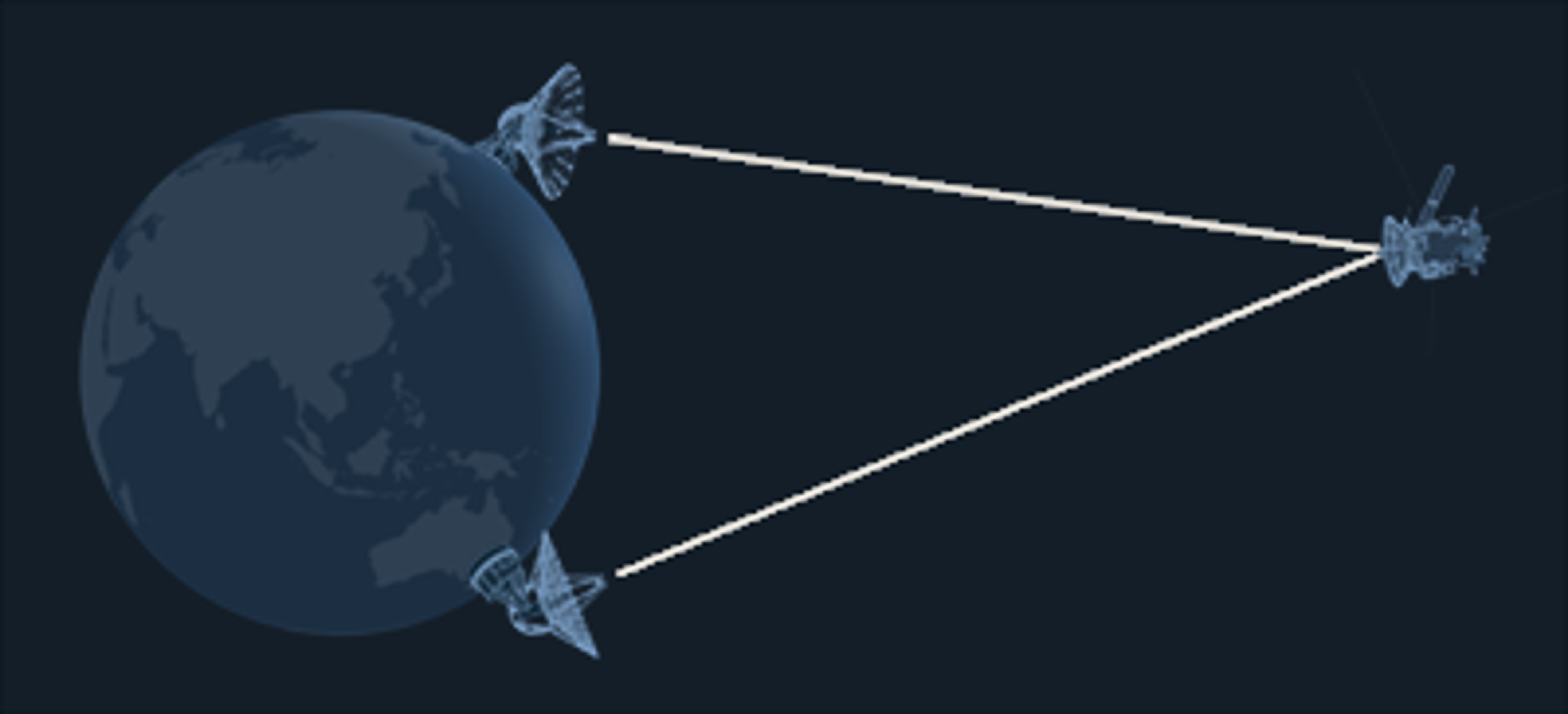
Extremely accurate angular measurements can be provided by a process independent from Doppler and range, called VLBI, Very Long Baseline Interferometry.

A VLBI observation of a spacecraft begins when two DSN stations on different continents (separated by a VLB) track a single spacecraft simultaneously. High-rate recordings are made of the downlink's wave fronts by each station, together with precise timing data. After a few minutes, both DSN antennas slew directly to the position of a quasar, which is an extragalactic object whose position on the plane of the sky is known to a high precision. Recordings are made of the quasar's radio-noise wave fronts.

Correlation and analysis of the recorded wave fronts yields a very precise triangulation from which the angular position may be determined by direct comparison to the position of a quasar whose RA and DEC are well known. VLBI is considered a distinct DSN data type, different from TRK and TLM. This VLBI observation of a spacecraft is called a "delta DOR," DOR meaning differenced one-way ranging (despite the fact that no range data is involved!), and the "delta" meaning the difference between spacecraft and quasar positions.

Precision Ranging

Precision ranging refers to a set of procedures to improve range measurements by using data from two stations that have a large north-south displacement, for example between California and Australia, via triangulation. Precision ranging can improve knowledge of the spacecraft's Declination as well.

Differenced Doppler

Differenced Doppler can provide a measure of a spacecraft's changing three-dimensional position. To visualize this, consider a spacecraft orbiting a distant planet as in the illustration of a Differenced Doppler. If the orbit is in a vertical plane exactly edge on to you at position A, you would observe the downlink to take a higher frequency as it travels towards you. As it recedes away from you to go behind the planet, you observe a lower frequency.

Now, imagine a second observer way across Earth, at position B. Since the orbit plane is not exactly edge-on as that observer sees it, that person will record a slightly different Doppler signature. If you and the other observer were to compare notes and difference your data sets, you would have enough information to determine both the spacecraft's changing velocity and position in three-dimensional space.

Two DSSs separated by a large baseline can do basically this. One DSS provides an uplink to the spacecraft so it can generate a coherent downlink, and then it receives two-way.

The other DSS receives a three-way coherent downlink. The differenced data sets are frequently called "two-way minus three-way."

These techniques, combined with high-precision knowledge of DSN Station positions, a precise characterization of atmospheric refraction and knowledge of the electron density in earth's ionosphere, plus extremely stable frequency and timing references (F&T, which is another one of the DSN data types), makes it possible for DSN to measure spacecraft velocities accurate to within hundredths of a millimeter per second, and angular position on the sky to within 10 nano-radians.

Doing the math to routinely get a very precise estimate of where the spacecraft is begins with an algorithm called the Batch Filter. It is up to orbit determination analysts to guide the algorithm and evaluate its results.

The process kicks off when the orbit determination team receives a new batch of tracking data from the DSN (the fact that the algorithm works on a set of data is what makes it a "batch" filter). For every distinct data point in the set, the algorithm constructs a corresponding "computed" data point. This computed point is essentially what that tracking data point should look like if the spacecraft were actually on the reference trajectory (this is where the mathematical relationship between the data point and spacecraft motion is exploited). The difference between the actual tracking data point and the computed point is called the residual, and it represents the degree to which the spacecraft has drifted from the reference orbit. A large residual indicates a large departure. Each data point in the set is differenced with its computed value, resulting in a set of residuals. The algorithm then adjusts its model of the spacecraft trajectory in such a way as to minimize the magnitude of the residual values. In this way, the starting reference trajectory is "bent" to match the actual trajectory. The trajectory which minimizes the residual values is considered to be the new "best estimate" of the spacecraft location.